Welcome to my Mathematics World

Volume

The volume of any solid, liquid, plasma, vacuum or theoretical object is how much three-dimensional space it occupies, often quantified numerically. One-dimensional figures (such as lines) and two-dimensional shapes (such as squares) are assigned zero volume in the three-dimensional space. Volume is commonly presented in units such as mL or cm3 (milliliters or cubic centimeters).

Volumes of some simple shapes, such as regular, straight-edged and circular shapes can be easily calculated using arithmetic formulas. More complicated shapes can be calculated by integral calculus if a formula exists for its boundary. The volume of any shape can be determined by displacement.

In differential geometry, volume is expressed by means of the volume form, and is an important global Riemannian invariant.

Volume is a fundamental parameter in thermodynamics and it is conjugate to pressure.

Related terms

The density of an object is defined as mass per unit volume. The inverse of density isspecific volume which is defined as volume divided by mass.

Volume and capacity are sometimes distinguished, with capacity being used for how much a container can hold (with contents measured commonly in liters or its derived units), and volume being how much space an object displaces (commonly measured in cubic metersor its derived units).

Volume and capacity are also distinguished in a capacity management setting, where capacity is defined as volume over a specified time period.

Traditional cooking measuresmeasureUSImperialmetric

teaspoon	1/6 U.S. fluid ounce (about 4.929 mL)	1/6 Imperial fluid ounce (about 4.736 mL)	5 mL
tablespoon = 3 teaspoons	½ U.S. fluid ounce (about 14.79 mL)	½ Imperial fluid ounce (about 14.21 mL)	15 mL
cup	8 U.S. fluid ounces or ½ U.S. liquid pint (about 237 mL)	8 Imperial fluid ounces or 2/5 fluid pint (about 227 mL)	250 mL

In the UK, a tablespoon can also be five fluidrams (about 17.76 mL).

Volume formulasShapeEquationVariables

A cube	$a^3;$	a = length of any side (or edge)
A rectangular prism:	$l cdot w cdot h$	l = length, w = width, h = height
A cylinder:	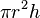$pi r^2 h;$	r = radius of circular face, h = height
A generalprism:	$B cdot h$	B = area of the base, h = height
A sphere:	$frac{4}{3} pi r^3$	r = radius of sphere which is the integral of the Surface Area of a sphere
Anellipsoid:	$frac{4}{3} pi abc$	a, b, c = semi-axes of ellipsoid
A pyramid:	$frac{1}{3}Ah$	A = area of the base, h = height of pyramid
A cone(circular-based pyramid):	$frac{1}{3} pi r^2 h$	r = radius of circle at base, h = distance from base to tip
Any figure (calculusrequired)	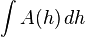$int A(h) ,dh$	h = any dimension of the figure, A(h) = area of the cross-sections perpendicular to h described as a function of the position along h. This will work for any figure if its cross-sectional area can be determined from h (no matter if the prism is slanted or the cross-sections change shape).

The units of volume depend on the units of length. If the lengths are in meters,
the volume will be in cubic meters.

Volume formula derivationSphere

The volume of a sphere is the integral of infinitesimal circular slabs of
thickness $dx$ . The calculation for the volume of a sphere with center 0
and radius $r$ is as follows.

The radius of the circular slabs is $y = sqrt{r^2-x^2}$

The surface area of the circular slab is $πy2$ .

The volume of the sphere can be calculated as $int_{-r}^r pi(r^2-x^2) ,dx = int_{-r}^r pi r^2,dx - int_{-r}^r pi x^2 ,dx$

Now $int_{-r}^r pi r^2,dx = 2pi r^3$ and $int_{-r}^r pi x^2 ,dx = 2 pi frac{r^3}{3}$

Combining yields $left(2-frac{2}{3}right)pi r^3 = frac{4}{3}pi r^3$

This formula can be derived more quickly using the formula for the sphere's
surface area, which is $4πr2$ . The volume of the sphere consists of layers of
infinitesimal spherical slabs, and the sphere volume is equal to

$int_0^r 4pi r^2 ,dr$ = $frac{4}{3}pi r^3$

Cone

The volume of a cone is the integral of infinitesimal circular slabs
of thickness $dx$ . The calculation for the volume of a cone of height $h$ ,
whose base is centered at (0,0) with radius $r$ is as follows.

The radius of each circular slab is $begin{cases} r, & mbox{if }mbox{ x=0} 0, & mbox{if }mbox{ x=h} end{cases}$ , and varying
linearly in between -- that is, $rfrac{(h-x)}{h}$

The surface area of the circular slab is then 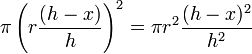$pi left(rfrac{(h-x)}{h}right)^2 = pi r^2frac{(h-x)^2}{h^2}$

The volume of the cone can then be calculated as $int_{0}^h pi r^2frac{(h-x)^2}{h^2} dx$

And after extraction of the constants: 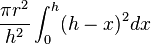$frac{pi r^2}{h^2} int_{0}^h (h-x)^2 dx$

Integrating gives us $frac{pi r^2}{h^2}left(frac{h^3}{3}right) = frac{1}{3}pi r^2 h$