En çok kullanılan matematiksel sabitler pi sayısı, e sayısı (doğal logaritma tabanı) ve i sayısıdır.

pi sayısı bir çemberin çevresinin çapına oranı ya da bir dairenin alanının yarıçap karesine oranı olarak ifade edilir.

e sayısı, Leonard Euler'in isminden gelir ve kabaca tanımı f(x) = 1/x fonksiyonunun eğrisi altında bir birim karelik alan sınırlanabilmesi için x=1 doğrusunun sağında seçilecek doğrunun x eksenini kestiği noktadır. Yani doğru x = e olarak seçilirse altta kalan şekil bir birim kare olacaktır. Bu eşitlik integral ile :

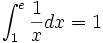 şeklinde ifade edilir. e sayısının başka bir tanımıysa bir dizi limiti tarafından verilir (integral Riemann toplamına açıldığında aslında iki tanımın özdeş oldureel sayılar]]dır. ğu ortaya çıkar.)

Pi ve e sayıları [[ i sayısı ise karmaşık sayıların tanımlanmasında kullanılan bir sabittir ve  olarak tanımlıdır.

Bunlar temel sabitler olup, bunların haricinde pek çok sabit bulunmaktadır.

== Bazı matematiksel sabitlerin tablosu ==-

 

Bazı Matematiksel Sabitler

Kullanılan kısaltmalar:

I - irraasyonel sayı, 
A - Cebirsel sayı, 
T - transendental sayı, Gen - General,
NuT - Sayılar Teorisi, 
ChT - Kaos Teorisi,
 Com - Kombinatorik, 
Inf - Information theory, 
Ana - Matematiksel Analiz 

SembolYaklaşık DeğerİsimAlanNKeşif YılıBilinen basamaklarının sayısı

π	≈ 3.14159 26535 89793 23846 26433 83279 50288	Pi, Archimedes' sabiti or Ludolph's number	Gen,Ana	T	by c. 2000 BC	1,241,100,000,000
e	≈ 2.71828 18284 59045 23536 02874 71352 66249	Napier's sabiti, base of Natural logarithm	Gen,Ana	T	1618	50,100,000,000
√2	≈ 1.41421 35623 73095 04880 16887 24209 69807	Pythagoras' sabiti,square root of two	Gen	I A	by c. 800 BC	137,438,953,444
√3	≈ 1.73205 08075 68877 29352 74463 41505	Theodorus' sabiti,square root of three	Gen	I A	by c. 800 BC
γ	≈ 0.57721 56649 01532 86060 65120 90082 40243	Euler-Mascheroni sabiti	Gen,NuT		1735	108,000,000
φ	≈ 1.61803 39887 49894 84820 45868 34365 63811	Golden mean	Gen	A	by 3rd century BC	3,141,000,000
β*	≈ 0.70258	Embree-Trefethen sabiti	NuT
δ	≈ 4.66920 16091 02990 67185 32038 20466 20161	Feigenbaum sabiti	ChT		1975
α	≈ 2.50290 78750 95892 82228 39028 73218 21578	Feigenbaum sabiti	ChT
C2	≈ 0.66016 18158 46869 57392 78121 10014 55577	Twin prime sabiti	NuT			5,020
M1	≈ 0.26149 72128 47642 78375 54268 38608 69585	Meissel-Mertens sabiti	NuT		1866 1874	8,010
B2	≈ 1.90216 05823	Brun's sabiti for twin prime	NuT		1919	10
B4	≈ 0.87058 83800	Brun's sabiti for prime quadruplets	NuT
Λ	> – 2.7 · 10-9	de Bruijn-Newman sabiti	NuT		1950?
K	≈ 0.91596 55941 77219 01505 46035 14932 38411	Catalan's sabiti	Com			201,000,000
K	≈ 0.76422 36535 89220 66	Landau-Ramanujan sabiti	NuT	I(?)		30,010
K	≈ 1.13198 824	Viswanath's sabiti	NuT			8
B´L	≈ 1.08366	Legendre's sabiti	NuT
μ	≈ 1.45136 92348 83381 05028 39684 85892 027	Ramanujan-Soldner sabiti	NuT			75,500
EB	≈ 1.60669 51524 15291 763	Erdős–Borwein sabiti	NuT	I
Ω	depends on computation model	Chaitin's sabiti	Inf	T
β	≈ 0.28016 94990	Bernstein's sabiti	Ana
λ	≈ 0.30366 30029	Gauss-Kuzmin-Wirsing sabiti	Com		1974	385
D(1)	≈ 0.35323 63719	Hafner-Sarnak-McCurley sabiti	NuT		1993
λ, μ	≈ 0.62432 99885	Golomb-Dickman sabiti	ComNuT		1930 1964
	≈ 0.62946 50204	Cahen's sabiti[1]
	≈ 0.66274 34193	Laplace limit
	≈ 0.80939 40205	Alladi-Grinstead sabiti	NuT
Λ	≈ 1.09868 58055	Lengyel's sabiti	Com		1992
	≈ 1.18656 91104	Khinchin-Lévy sabiti	NuT
	≈ 1.20205 69031 59594 28539 97381	Apéry's sabiti			1979	1,000,000,000
θ	≈ 1.30637 78838 63080 69046	Mills' sabiti	NuT	?	1947
	≈ 1.45607 49485 82689 67139 95953 51116 54356	Backhouse's sabiti
	≈ 1.46707 80794	Porter's sabiti[2]	NuT		1975
	≈ 1.53960 07178	Lieb's square ice sabiti	Com		1967
	≈ 1.70521 11401 05367	Niven's sabiti[3]	NuT		1969
	≈ 2.58498 17596	Sierpiński's sabiti[4]
	≈ 2.68545 2001	Khinchin's sabiti[5]	NuT	?	1934	7350
F	≈ 2.80777 02420	Fransén-Robinson sabiti[6]	Ana
L	≈ .5	Landau's sabiti	Ana			1