The name of the Greek letter π is pi, and this spelling is commonly used in typographicalcontexts when the Greek letter is not available, or its usage could be problematic. When referring to this constant, the symbol π is always pronounced like "pie" in English, which is the conventional English pronunciation of the Greek letter. In Greek, the name of this letter is pronounced /pi/.

The constant is named "π" because "π" is the first letter of the Greek words περιφέρεια (periphery) and περίμετρος (perimeter), probably referring to its use in the formula to find the circumference, or perimeter, of a circle.[2] π is Unicode character U+03C0 ("Greek small letter pi").[3]

 

Circumference = π × diameter

In Euclidean plane geometry, π is defined as the ratio of a circle's circumference to itsdiameter:[2]

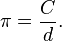
The ratio C/d is constant, regardless of a circle's size. For example, if a circle has twice the diameter d of another circle it will also have twice the circumference C, preserving the ratio C/d. This fact is a consequence of the similarity of all circles.

 

Area of the circle = π × area of the shaded square

Alternatively π can be also defined as the ratio of a circle's area (A) to the area of a square whose side is equal to the radius:[2][4]

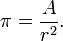
The constant π may be defined in other ways that avoid the concepts of arc length and area, for example, as twice the smallest positive x for which cos(x) = 0.[5] The formulas below illustrate other (equivalent) definitions.

Being an irrational number, π cannot be written as the ratio of two integers. This was proven in 1761 by Johann Heinrich Lambert.[2] In the 20th century, proofs were found that require no prerequisite knowledge beyond integral calculus. One of those, due to Ivan Niven, is widely known.[6][7] A somewhat earlier similar proof is by Mary Cartwright.[8]

Furthermore, π is also transcendental, as was proven by Ferdinand von Lindemann in 1882. This means that there is no polynomial with rational coefficients of which π is aroot.[9] An important consequence of the transcendence of π is the fact that it is notconstructible. Because the coordinates of all points that can be constructed with compass and straightedge are constructible numbers, it is impossible to square the circle: that is, it is impossible to construct, using compass and straightedge alone, a square whose area is equal to the area of a given circle.[10] This is historically significant, for squaring a circle is one of the easily understood elementary geometry problems left to us from antiquity; many amateurs in modern times have attempted to solve each of these problems, and their efforts are sometimes ingenious, but in this case, doomed to failure: a fact not always understood by the amateur involved.

The numerical value of π truncated to 50 decimal places is:[11]

While the value of π has been computed to more than a trillion (1012) digits,[12]elementary applications, such as calculating the circumference of a circle, will rarely require more than a dozen decimal places. For example, a value truncated to 11 decimal places is accurate enough to calculate the circumference of the earth with a precision of a millimeter, and one truncated to 39 decimal places is sufficient to compute the circumference of any circle that fits in the observable universe to a precision comparable to the size of a hydrogen atom.[13][14]

Because π is an irrational number, its decimal expansion never ends and does not repeat. This infinite sequence of digits has fascinated mathematicians and laymen alike, and much effort over the last few centuries has been put into computing more digits and investigating the number's properties.[15] Despite much analytical work, and supercomputercalculations that have determined over 1 trillion digits of π, no simple pattern in the digits has ever been found.[16] Digits of π are available on many web pages, and there issoftware for calculating π to billions of digits on any personal computer.

π can be empirically estimated by drawing a large circle, then measuring its diameter and circumference and dividing the circumference by the diameter. Another geometry-based approach, due to Archimedes,[17] is to calculate the perimeter, Pn , of a regular polygonwith n sides circumscribed around a circle with diameter d. Then

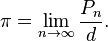
That is, the more sides the polygon has, the closer the approximation approaches π. Archimedes determined the accuracy of this approach by comparing the perimeter of the circumscribed polygon with the perimeter of a regular polygon with the same number of sides inscribed inside the circle. Using a polygon with 96 sides, he computed the fractional range: .[18]

π can also be calculated using purely mathematical methods. Most formulas used for calculating the value of π have desirable mathematical properties, but are difficult to understand without a background in trigonometry and calculus. However, some are quite simple, such as this form of the Gregory-Leibniz series:[19]

While that series is easy to write and calculate, it is not immediately obvious why it yields π. In addition, this series converges so slowly that 300 terms are not sufficient to calculateπ correctly to 2 decimal places.[20] However, by computing this series in a somewhat more clever way by taking the midpoints of partial sums, it can be made to converge much faster. Let

and then define

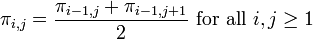
then computing π10,10 will take similar computation time to computing 150 terms of the original series in a brute-force manner, and , correct to 9 decimal places. This computation is an example of the Van Wijngaarden transformation.[21]

The history of π parallels the development of mathematics as a whole.[22] Some authors divide progress into three periods: the ancient period during which π was studied geometrically, the classical era following the development of calculus in Europe around the 17th century, and the age of digital computers.[23]

That the ratio of the circumference to the diameter of a circle is the same for all circles, and that it is slightly more than 3, was known to ancient Egyptian, Babylonian, Indian and Greek geometers. The earliest known approximations date from around 1900 BC; they are 25/8 (Babylonia) and 256/81 (Egypt), both within 1% of the true value.[2] The Indian textShatapatha Brahmana gives π as 339/108 ≈ 3.139. The Tanakh appears to suggest, in the Book of Kings, that π = 3, which is notably worse than other estimates available at the time of writing (600 BC). The interpretation of the passage is disputed,[24][25] as some believe the ratio of 3:1 is of an interior circumference to an exterior diameter of a thinly walled basin, which could indeed be an accurate ratio, depending on the thickness of the walls (See: Biblical value of π).

Archimedes (287-212 BC) was the first to estimate π rigorously. He realized that its magnitude can be bounded from below and above by inscribing circles in regular polygonsand calculating the outer and inner polygons' respective perimeters:[25]

 

Liu Hui's π algorithm

By using the equivalent of 96-sided polygons, he proved that 223/71 < π < 22/7.[25] 
Taking the average of these values yields 3.1419.

In the following centuries further development took place in India and China. Around 
265, the Wei Kingdom mathematician Liu Hui provided a simple and rigorous iterative algorithm to calculate π to any degree of accuracy. He himself carried through the 
calculation to a 3072-gon and obtained an approximate value for π of 3.1416.

Later, Liu Hui invented a quick method of calculating π and obtained an approximate 
value of 3.1416 with only a 96-gon, by taking advantage of the fact that the difference 
in area of successive polygons forms a geometric series with a factor of 4.

Around 480, the Chinese mathematician Zu Chongzhi demonstrated that π ≈ 355/113, 
and showed that 3.1415926 < π < 3.1415927 using Liu Hui's algorithm applied to a 
12288-gon. This value was the most accurate approximation of π available for next 
900 years.

Until the second millennium, π was known to fewer than 10 decimal digits. The next major advance in π studies came with the development of calculus, and in particular the discovery of infinite series which in principle permit calculating π to any desired accuracy by adding sufficiently many terms. Around 1400, Madhava of Sangamagrama found the first known such series:

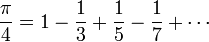
This is now known as the Madhava-Leibniz series[26][27] or Gregory-Leibniz series since it was rediscovered by James Gregory and Gottfried Leibniz in the 17th century. Unfortunately, the rate of convergence is too slow to calculate many digits in practice; about 4,000 terms must be summed to improve upon Archimedes' estimate. However, by transforming the series into

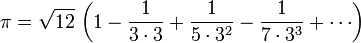
Madhava was able to calculate π as 3.14159265359, correct to 11 decimal places. The 
record was beaten in 1424 by the Persian mathematician, Jamshīd al-Kāshī, who 
determined 16 decimals of π.

The first major European contribution since Archimedes was made by the German mathematician Ludolph van Ceulen (1540–1610), who used a geometric method to 
compute 35 decimals of π. He was so proud of the calculation, which required the 
greater part of his life, that he had the digits engraved into his tombstone.[28]

Around the same time, the methods of calculus and determination of infinite series and products for geometrical quantities began to emerge in Europe. The first such 
representation was the Viète's formula,

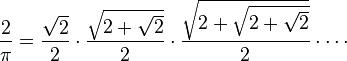
found by François Viète in 1593. Another famous result is Wallis' product,

by John Wallis in 1655. Isaac Newton himself derived a series for π and calculated 
15 digits, although he later confessed: "I am ashamed to tell you to how many figures
 I carried these computations, having no other business at the time." [29]

In 1706 John Machin was the first to compute 100 decimals of π, using the formula

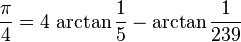
with

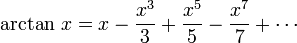
Formulas of this type, now known as Machin-like formulas, were used to set several successive records and remained the best known method for calculating π well into the age of computers. A remarkable record was set by the calculating prodigy Zacharias Dase, who in 1844 employed a Machin-like formula to calculate 200 decimals of π in his head at the behest of Gauss. The best value at the end of the 19th century was due to William Shanks, who took 15 years to calculate π with 707 digits, although due to a mistake only the first 527 were correct. (To avoid such errors, modern record calculations of any kind are often performed twice, with two different formulas. If the results are the same, they are likely to be correct.)

Theoretical advances in the 18th century led to insights about π's nature that could not be achieved through numerical calculation alone. Johann Heinrich Lambert proved the irrationality of π in 1761, and Adrien-Marie Legendre also proved in 1794 π2 to be irrational. When Leonhard Euler in 1735 solved the famous Basel problem – finding the exact value of

which is π2/6, he established a deep connection between π and the prime numbers. Both Legendre and Leonhard Euler speculated that π might be transcendental, which was finally proved in 1882 by Ferdinand von Lindemann.

William Jones' book A New Introduction to Mathematics from 1706 is said to be the first use of the Greek letter π for this constant, but the notation became particularly popular after Leonhard Euler adopted it in 1737.[30] He wrote:

The advent of digital computers in the 20th century led to an increased rate of new π calculation records. John von Neumann used ENIAC to compute 2037 digits of π in 1949, a calculation that took 70 hours. Additional thousands of decimal places were obtained in the following decades, with the million-digit milestone passed in 1973. Progress was not only due to faster hardware, but also new algorithms. One of the most significant developments was the discovery of the fast Fourier transform (FFT) in the 1960s, which allows computers to perform arithmetic on extremely large numbers quickly.

In the beginning of the 20th century, the Indian mathematician Srinivasa Ramanujan found many new formulas for π, some remarkable for their elegance and mathematical depth.[31]Two of his most famous formulas are the series

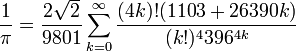
and

which deliver 14 digits per term.[31] The Chudnovsky brothers used this formula to set several π computing records in the end of the 1980s, including the first calculation of over one billion (1,011,196,691) decimals in 1989. It remains the formula of choice for π calculating software that runs on personal computers, as opposed to the supercomputersused to set modern records.

Whereas series typically increase the accuracy with a fixed amount for each added term, there exist iterative algorithms that multiply the number of correct digits at each step, with the downside that each step generally requires an expensive calculation. A breakthrough was made in 1975, when Richard Brent and Eugene Salamin independently discovered theBrent–Salamin algorithm, which uses only arithmetic to double the number of correct digits at each step.[32] The algorithm consists of setting

and iterating

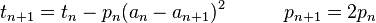
until an and bn are close enough. Then the estimate for π is given by

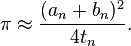
Using this scheme, 25 iterations suffice to reach 45 million correct decimals. A similar algorithm that quadruples the accuracy in each step has been found by Jonathan andPeter Borwein.[33] The methods have been used by Yasumasa Kanada and team to set most of the π calculation records since 1980, up to a calculation of 206,158,430,000 decimals of π in 1999. The current record is 1,241,100,000,000 decimals, set by Kanada and team in 2002. Although most of Kanada's previous records were set using the Brent-Salamin algorithm, the 2002 calculation made use of two Machin-like formulas that were slower but crucially reduced memory consumption. The calculation was performed on a 64-node Hitachi supercomputer with 1 terabyte of main memory, capable of carrying out 2 trillion operations per second.

An important recent development was the Bailey–Borwein–Plouffe formula (BBP formula), discovered by Simon Plouffe and named after the authors of the paper in which the formula was first published, David H. Bailey, Peter Borwein, and Plouffe.[34] The formula,

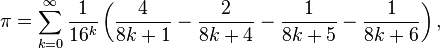
is remarkable because it allows extracting any individual hexadecimal or binary digit of π without calculating all the preceding ones.[34] Between 1998 and 2000, the distributed computing project PiHex used a modification of the BBP formula due to Fabrice Bellard to compute the quadrillionth (1,000,000,000,000,000:th) bit of π, which turned out to be 0.[35]

Even long before computers have calculated π, memorizing a record number of digits became an obsession for some people. In 2006, Akira Haraguchi, a retired Japanese engineer, claimed to have recited 100,000 decimal places.[36] This, however, has yet to be verified by Guinness World Records. The Guinness-recognized record for remembered digits of π is 67,890 digits, held by Lu Chao, a 24-year-old graduate student fromChina.[37] It took him 24 hours and 4 minutes to recite to the 67,890th decimal place of π without an error.[38]

There are many ways to memorize π, including the use of "piems", which are poems that represent π in a way such that the length of each word (in letters) represents a digit. Here is an example of a piem: How I need a drink, alcoholic in nature (or: of course), after the heavy lectures involving quantum mechanics.[39] Notice how the first word has 3 letters, the second word has 1, the third has 4, the fourth has 1, the fifth has 5, and so on. TheCadaeic Cadenza contains the first 3834 digits of π in this manner.[40] Piems are related to the entire field of humorous yet serious study that involves the use of mnemonic techniques to remember the digits of π, known as piphilology. See Pi mnemonics for examples. In other languages there are similar methods of memorization. However, this method proves inefficient for large memorizations of π. Other methods include remembering patterns in the numbers.[41]