Welcome to my Mathematics World

Area (Alan)

Area is a quantity expressing the two-dimensional size of a defined part of a surface, typically a region bounded by a closed curve. The term surface area refers to the total area of the exposed surface of a 3-dimensional solid, such as the sum of the areas of the exposed sides of a polyhedron. Area is an important invariant in the differential geometry of surfaces.

area (a) = 100 square meters (m²) hectare (ha) = 100 ares (a) = 10000 square meters (m²)square kilometre (km²) = 100 hectars (ha) = 10000 ares (a) = 1000000 square metres (m²)square megametre (Mm²) = 1012 square metres square foot = 144 square inches = 0.09290304 square metres (m²) square yard = 9 square feet (0.84 m2) = 0.83612736 square metres (m²) square perch = 30.25 square yards = 25.2928526 square metres (m²) acre = 10 square chains (also one furlong by one chain); or 160 square perches; or 4840 square yards; or 43,560 square feet (4,047 m2) = 4046.8564224 square metres (m²) square mile = 640 acres (2.6 km2) = 2.5899881103 square kilometers (km²)

Formula

Common formula for area:ShapeEquationVariables

Square	$s^2,!$	$s$ is the length of one side of the square.
Regular triangle(equilateral triangle)	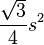$frac{sqrt{3}}{4}s^2,!$	$s$ is the length of one side of the triangle.
Regular hexagon	$frac{3sqrt{3}}{2}s^2,!$	$s$ is the length of one side of the hexagon.
Regular octagon	$2left(1+sqrt{2}right)s^2,!$	$s$ is the length of one side of the octagon.
Any regular polygon	$frac{1}{2}a p ,!$	$a$ is the apothem, or the radius of an inscribed circle in the polygon, and $p$ is the perimeter of the polygon.
Any regular polygon	$frac{ns^2} {4 cdot tan(pi/n)},!$	$s$ is the sidelength and $n$ is the number of sides.
Any regular polygon (using degree measure)	$frac{ns^2} {4 cdot tan(180^circ/n)},!$	$s$ is the sidelength and $n$ is the number of sides.
Rectangle	$lw ,!$	$l$ and $w$ are the lengths of the rectangle's sides (length and width).
Parallelogram (in general)	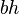$bh,!$	$b$ and $h$ are the length of the base and the length of the perpendicular height, respectively.
Rhombus	$frac{1}{2}ab$	$a$ and $b$ are the lengths of the twodiagonals of the rhombus.
Triangle	$frac{1}{2}bh ,!$	$b$ and $h$ are the base and altitude(measured perpendicular to the base), respectively.
Triangle	$frac{1}{2} a b sin(C),!$	$a$ and $b$ are any two sides, and $C$ is the angle between them.
Circle	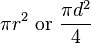$pi r^2 text{or} frac{pi d^2}{4} ,!$	$r$ is the radius and $d$ the diameter.
Ellipse	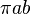$pi ab ,!$	$a$ and $b$ are the semi-major and semi-minor axes, respectively.
Trapezoid	$frac{1}{2}(a+b)h ,!$	$a$ and $b$ are the parallel sides and $h$ the distance (height) between the parallels.
Total surface area of aCylinder	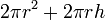$2pi r^2+2pi r h ,!$	$r$ and $h$ are the radius and height, respectively.
Lateral surface area of a cylinder	$2 pi r h ,!$	$r$ and $h$ are the radius and height, respectively.
Total surface area of aCone	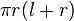$pi r (l + r) ,!$	$r$ and $l$ are the radius and slant height, respectively.
Lateral surface area of a cone	$pi r l ,!$	$r$ and $l$ are the radius and slant height, respectively.
Total surface area of aSphere	$4pi r^2 text{or} 2pi d^2,!$	$r$ and $d$ are the radius and diameter, respectively.
Total surface area of an ellipsoid		See the article.
Circular sector	$frac{1}{2} r^2 theta ,!$	$r$ and $θ$ are the radius and angle (inradians), respectively.
Square to circular area conversion	$frac{4}{pi} A,!$	$A$ is the area of the square in square units.
Circular to square area conversion	$frac{1}{4} Cpi,!$	$C$ is the area of the circle in circular units.

All of the above calculations show how to find the area of many common shapes.

The area of irregular polygons can be calculated using the "Surveyor's formula".[1]

How to define area

Area is a quantity expressing the size of the contents of a region on a 2-dimensional surface. Points and lines have zero area, cf. space-filling curves. A region may have infinite area, for example the entire Euclidean plane. The 3-dimensional analog of area is volume. Although area seems to be one of the basic notions in geometry, it is not easy to define even in the Euclidean plane. Most textbooks avoid defining an area, relying on self-evidence. For polygons in the Euclidean plane, one can proceed as follows:

The area of a polygon in the Euclidean plane is a positive number such that:

The area of the unit square is equal to one.
Congruent polygons have equal areas.
(additivity) If a polygon is a union of two polygons which do not have common interior points, then its area is the sum of the areas of these polygons.

It remains to show that the notion of area thus defined does not depend on the way one subdivides a polygon into smaller parts.

A typical way to introduce area is through the more advanced notion of Lebesgue measure. In the presence of the axiom of choice it is possible to prove the existence of shapes whose Lebesgue measure cannot be meaningfully defined. Such 'shapes' (they cannot a fortiori be simply visualised) enter into Tarski's circle-squaring problem (and, moving to three dimensions, in the Banach–Tarski paradox). The sets involved do not arise in practical matters.

In three dimensions, the analog of area is called volume. The n dimensional analog, usually referred to as 'content', is defined by means of a measure or as a Lebesgue integral.

Additional formulasAreas of 2-dimensional figures

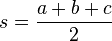a triangle: $frac{Bh}{2}$ (where B is any side, and h is the distance from the line on which B lies to the other vertex of the triangle). This formula can be used if the height h is known. If the lengths of the three sides are known then Heron's formula can be used: $sqrt{s(s-a)(s-b)(s-c)}$ (where a, b, c are the sides of the triangle, and $s = frac{a + b + c}{2}$ is half of its perimeter) If an angle and its two included sides are given, then area=absinC where C is the given angle and a and b are its included sides. If the triangle is graphed on a coordinate plane, a matrix can be used and is simplified to the absolute value of (x1y2+ x2y3+ x3y1 - x2y1- x3y2- x1y3) all divided by 2. This formula is also known as the shoelace formula and is an easy way to solve for the area of a coordinate triangle by substituting the 3 points, (x1,y1) (x2,y2) (x3,y 3). The shoelace formula can also be used to find the areas of other polygons when their vertices are known. Another approach for a coordinate triangle is to use Infinitesimal calculus to find the area.

Area in calculus

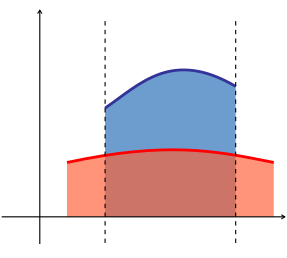
The area between two graphs can be evaluated by calculating the difference between the integrals of the two functions

the area between the graphs of two functions is equal to the integral of one function, f(x),minus the integral of the other function, g(x).
an area bounded by a function r = r(θ) expressed in polar coordinates is ${1 over 2} int_0^{2pi} r^2 , dtheta$ .
the area enclosed by a parametric curve $vec u(t) = (x(t), y(t))$ with endpoints $vec u(t_0) = vec u(t_1)$ is given by the line integrals

$oint_{t_0}^{t_1} x dot y , dt = - oint_{t_0}^{t_1} y dot x , dt = {1 over 2} oint_{t_0}^{t_1} (x dot y - y dot x) , dt$

(see Green's theorem)

or the z-component of ${1 over 2} oint_{t_0}^{t_1} vec u times dot{vec u} , dt.$

Surface area of 3-dimensional figures

cube: $6s2$ , where s is the length of the top side
rectangular box: 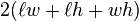$2 (ell w + ell h + w h)$ the length divided by height
cone: $pi rleft(r + sqrt{r^2 + h^2}right)$ , where r is the radius of the circular base, and h is the height. That can also be rewritten as $πr2 + πrl$ where r is the radius and l is the slant height of the cone. $πr2$ is the base area while $πrl$ is the lateral surface area of the cone.
prism: 2 * Area of Base + Perimeter of Base * Height

General formula

The general formula for the surface area of the graph of a continuously differentiable function $z = f(x,y),$ where 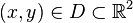$(x,y)in Dsubsetmathbb{R}^2$ and $D$ is a region in the xy-plane with the smooth boundary:

$A=iint_Dsqrt{left(frac{partial f}{partial x}right)^2+left(frac{partial f}{partial y}right)^2+1},dx,dy.$

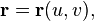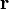Even more general formula for the area of the graph of a parametric surface in the vector form $mathbf{r}=mathbf{r}(u,v),$ where $mathbf{r}$ is a continuously differentiable vector function of $(u,v)in Dsubsetmathbb{R}^2$ :

$A=iint_D left|frac{partialmathbf{r}}{partial u}timesfrac{partialmathbf{r}}{partial v}right|,du,dv.$

Area minimisation

Given a wire contour, the surface of least area spanning ("filling") it is a minimal surface. Familiar examples include soap bubbles.

The question of the filling area of the Riemannian circle remains open.