Welcome to my Mathematics World

In mathematics, the binomial theorem is an important formula giving the expansion ofpowers of sums. Its simplest version states that

$(x+y)^n=sum_{k=0}^n{n choose k}x^{n-k}y^{k}quadquadquad(1)$

for any real or complex numbers x and y, and any non-negative integer n. The binomial coefficient appearing in (1) may be defined in terms of the factorial function n!:

${n choose k}=frac{n!}{k!,(n-k)!}.$

Examples

Taking n to be 2, 3, 4, or 5 in the binomial theorem yields

$begin{align} (x + y)^2 & = x^2 + 2xy + y^2 [6pt] (x + y)^3 & = x^3 + 3x^2y + 3xy^2 + y^3 [6pt] (x + y)^4 & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4 [6pt] (x + y)^5 & = x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 +5xy^4 + y^5. end{align}$

Combinatorial proof

Example

The coefficient of $xy2$ in

$(x + y)3 = (x + y)(x + y)(x + y) = xxx + xxy + xyx + xyy + yxx + yxy + yyx + yyy = x3 + 3x2y + 3xy2 + y3.$

equals $binom{3}{2}=3$ because there are three x,y strings of length 3 with exactly
two y's, namely,

$xyy, ; yxy, ; yyx,$

corresponding to the three 2-element subsets of ${1,2,3}$ , namely,

${2,3},;{1,3},;{1,2},$

where each subset specifies the positions of the y in a corresponding string.

General case

Expanding $(x + y)n$ yields the sum of the $2n$ products of the form $e_1 e_2 cdots e_n$
where each $ei$ is x or y. Rearranging factors shows that each product equals
$xn - kyk$ for some k between 0 and n. For a given k, the following are proved
equal in succession:

the number of copies of $xn - kyk$ in the expansion
the number of n-character x,y strings having y in exactly k positions
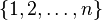
the number of k-element subsets of ${1,2,ldots,n}$
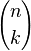${n choose k}$ (this is either by definition, or by a short combinatorial argument
if one is defining 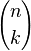${n choose k}$ as $frac{n!}{k!,(n-k)!}$ ).

This proves the binomial theorem.

Inductive proof

Another way to prove the binomial theorem (1) is with mathematical induction.
When n = 0, we have

$(a+b)^0 = 1 = sum_{k=0}^0 { 0 choose k } a^{0-k}b^k.$

For the inductive step, assume the theorem holds when the exponent is m.
Then for n = m + 1

$(a+b)^{m+1} = a(a+b)^m + b(a+b)^m ,$

$= a sum_{k=0}^m { m choose k } a^{m-k} b^k + b sum_{j=0}^m { m choose j } a^{m-j} b^j$

by the inductive hypothesis

$= sum_{k=0}^m { m choose k } a^{m-k+1} b^k + sum_{j=0}^m { m choose j } a^{m-j} b^{j+1}$

by multiplying through by a and b

$= a^{m+1} + sum_{k=1}^m { m choose k } a^{m-k+1} b^k + sum_{j=0}^m { m choose j } a^{m-j} b^{j+1}$

by pulling out the k = 0 term

$= a^{m+1} + sum_{k=1}^m { m choose k } a^{m-k+1} b^k + sum_{k=1}^{m+1} { m choose k-1 }a^{m-k+1}b^{k}$

by letting j = k − 1

$= a^{m+1} + sum_{k=1}^m { m choose k } a^{m-k+1}b^k + sum_{k=1}^{m} { m choose k-1 }a^{m+1-k}b^{k} + b^{m+1}$

by pulling out the k = m + 1 term from the right hand side

$= a^{m+1} + b^{m+1} + sum_{k=1}^m left[ { m choose k } + { m choose k-1 } right] a^{m+1-k}b^k$

by combining the sums

$= a^{m+1} + b^{m+1} + sum_{k=1}^m { m+1 choose k } a^{m+1-k}b^k$

from Pascal's rule

$= sum_{k=0}^{m+1} { m+1 choose k } a^{m+1-k}b^k$

by adding in the 0 and m + 1 terms.

Newton's generalized binomial theorem

Around 1665, Isaac Newton generalized the formula to allow exponents other than nonnegative integers. In this generalization, the finite sum is replaced by an infinite series. Namely, if x and y are real numbers with x > |y|,[1] and r is any complex number, then

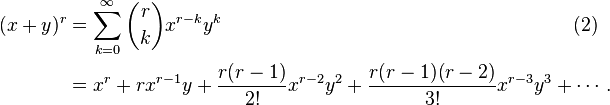
$begin{align} (x+y)^r & =sum_{k=0}^infty {r choose k} x^{r-k} y^k qquadqquadqquadqquadqquadqquadqquadqquadqquad(2) & = x^r + r x^{r-1} y + frac{r(r-1)}{2!} x^{r-2} y^2 + frac{r(r-1)(r-2)}{3!} x^{r-3} y^3 + cdots. end{align}$

When r is a nonnegative integer, the binomial coefficients for k > r are zero, so (2) specializes to (1), and there are at most r+1 nonzero terms. For other values of r, the series (2) has an infinite number of nonzero terms, at least if x and y are nonzero.

The coefficients can also be written

${r choose k}=frac{(r)_k}{k!},$

where $(cdot)_k$ is the Pochhammer symbol. This is important when one is working with infinite series and would like to represent them in terms of generalized hypergeometric functions. This form is used in applied mathematics, for example, when evaluating the formulas that model the statistical properties of the phase-front curvature of a light wave as it propagates through optical atmospheric turbulence.[citation needed]

Taking r = −s leads to a particularly handy but non-obvious formula:

$frac{1}{(1-x)^s}=sum_{k=0}^infty {s+k-1 choose k} x^k equiv sum_{k=0}^infty {s+k-1 choose s-1} x^k.$

Further specializing to s = 1 yields the geometric series formula.

Generalizations

Formula (2) can be generalized to the case where x and y are complex numbers. For this version, one should assume |x| > |y|[1] and define the powers of x + y and x using aholomorphic branch of log defined on an open disk of radius |x| centered at x.

Formula (2) is valid also for elements x and y of a Banach algebra as long as xy = yx, x is invertible, and ||y/x|| < 1.

For a more extensive account of Newton's generalized binomial theorem, see binomial series.

The binomial theorem in abstract algebra

Formula (1) is valid more generally for any elements x and y of a semiring satisfying xy = yx. The theorem is true even more generally: alternativity suffices in place ofassociativity.

The binomial theorem can be stated by saying that the polynomial sequence $left{1,x,x^2,x^3,dotsright}$ is of binomial type.

History

This formula and the triangular arrangement of the binomial coefficients are often attributed to Blaise Pascal, who described them in the 17th century, but they were known to many mathematicians who preceded him. The 4th century B.C. Greek mathematician Euclidknew a special case of the binomial theorem up to the second order,[2][3] as did the 3rd century B.C. Indian mathematician Pingala to higher orders. A more general binomial theorem and the so-called "Pascal's triangle" were known to the 10th-century A.D. Indian mathematician Halayudha, the 11th-century A.D. Persian mathematician Omar Khayyám, and 13th-century Chinese mathematician Yang Hui, who all derived similar results.[4]