Welcome to my Mathematics World - Cauchy İntegral Teoremi

Cauchy's integral theorem

In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane. Essentially, it says that if two different paths connect the same two points, and a function is holomorphic everywhere "in between" the two paths, then the two path integrals of the function will be the same.

The theorem is usually formulated for closed paths as follows: let U be an open subset of Cwhich is simply connected, let f : U → C be a holomorphic function, and let $!,gamma$ be arectifiable path in U whose start point is equal to its end point. Then,

$oint_gamma f(z),dz = 0.$

As was shown by Goursat, Cauchy's integral theorem can be proven assuming only that the complex derivative f '(z) exists everywhere in U. This is significant, because one can then prove Cauchy's integral formula for these functions, and from that one can deduce that these functions are in fact infinitely differentiable.

The condition that U be simply connected means that U has no "holes" or, in homotopyterms, that the fundamental group of U is trivial; for instance, every open disk $U = {z: | z - z0 | < r}$ qualifies. The condition is crucial; consider

$gamma(t) = e^{it} quad t in left[0,2piright]$

which traces out the unit circle, and then the path integral

$oint_gamma frac{1}{z},dz = int_0^{2pi} { ie^{it} over e^{it} },dt= int_0^{2pi}i,dt = 2pi i$

is non-zero; the Cauchy integral theorem does not apply here since $f(z) = 1 / z$ is not defined (and certainly not holomorphic) at $z = 0$ .

One important consequence of the theorem is that path integrals of holomorphic functions on simply connected domains can be computed in a manner familiar from the fundamental theorem of real calculus: let U be a simply connected open subset of C, let f : U → C be a holomorphic function, and let γ be a piecewise continuously differentiable path in U with start point a and end point b. If F is a complex antiderivative of f, then

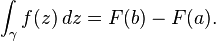
$int_gamma f(z),dz=F(b)-F(a).$

The Cauchy integral theorem is valid in a slightly stronger form than given above. Suppose U is an open simply connected subset of C whose boundary is the image of the rectifiable path $!,gamma$ . If f is a function which is holomorphic on U and continuous on the closure of U, then

$oint_gamma f(z),dz=0.$

The Cauchy integral theorem leads to Cauchy's integral formula and the residue theorem.