In mathematics, an imaginary number (or purely imaginary number) is a complex number whose squared value is a real number not greater than zero.[1] The imaginary unit, denoted by i or j, is an example of an imaginary number. If y is a real number, then i·y is an imaginary number, because:
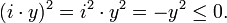
Imaginary numbers were defined in 1572 by Rafael Bombelli. At the time, such numbers were thought not to exist, much as zero and the negative numbers were regarded by some as fictitious or useless. Many other mathematicians were slow to believe in imaginary numbers at first, including Descartes who wrote about them in his La Géométrie, where the term was meant to be derogatory.[2]
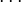 (repeats the pattern (repeats the pattern
from blue area) |
 |
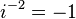 |
 |
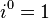 |
 |
 |
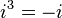 |
 |
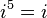 |
 |
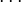 (repeats the pattern (repeats the pattern
from blue area) |
Although Descartes originally used the term imaginary number to mean what is currently meant by the term complex number, the term imaginary number today usually means a complex number with a real part equal to 0, that is, a number of the form i·y. Zero (0) is the only number that is both real and imaginary.[1]
Geometric interpretation
Geometrically, imaginary numbers are found on the vertical axis of the complex number plane, allowing them to be presented orthogonal to the real axis. One way of viewing imaginary numbers is to consider a standard number line, positively increasing in magnitude to the right, and negatively increasing in magnitude to the left. At 0 on this x-axis, a y-axis can be drawn with "positive" direction going up; "positive" imaginary numbers then "increase" in magnitude upwards, and "negative" imaginary numbers "decrease" in magnitude downwards. This vertical axis is often called the "imaginary axis" and is denoted ,
,  or simply Im.
or simply Im.
In this representation, multiplication by −1 corresponds to a rotation of 180 degrees about the origin. Multiplication by i corresponds to a 90-degree rotation in the "positive" direction (i.e. counter-clockwise), and the equation i2 = − 1 is interpreted as saying that if we apply 2 90-degree rotations about the origin, the net result is a single 180-degree rotation. Note that a 90-degree rotation in the "negative" direction (i.e. clockwise) also satisfies this interpretation. This reflects the fact that −i also solves the equation x2 = − 1 — seeimaginary unit.
Applications of imaginary numbers
For most human tasks, real numbers (or even rational numbers) offer an adequate description of data. Fractions such as ⅔ and ⅛ are meaningless to a person counting stones, but essential to a person comparing the sizes of different collections of stones. Negative numbers such as −3 and −5 are meaningless when weighing the mass of an object, but essential when keeping track of monetary debits and credits[2]. Similarly, imaginary numbers have essential concrete applications in a variety of sciences and related areas such as signal processing, control theory, electromagnetism, quantum mechanics, cartography, vibration analysis and many others.
In electrical engineering, for example, the voltage produced by a battery is characterized by one real number (called amplitude), such as +12 volts or −12 volts. But the "AC" voltage in a home requires two parameters. One is an amplitude, such as 120 volts, and the other is an angle (called phase). The voltage is said to have two dimensions. A 2-dimensional quantity can be represented mathematically as either a vector or as a complex number (known in the engineering context as phasor). In the vector representation, the rectangularcoordinates are typically referred to simply as X and Y. But in the complex number representation, the same components are referred to as real and imaginary. When the complex number is purely imaginary, such as a real part of 0 and an imaginary part of 120, it means the voltage has an amplitude of 120 volts and a phase of 90°, which is physically very real.
Some programming languages have built-in support for imaginary numbers. For example, in the Python interpreter, one may use them by appending a lowercase or uppercase J to the number[3]:
>>> (5+2j) * (8+5j) (30+41j)
Matlab examples:
>> (5+2j) * (8+5j) ans = 30.0000 +41.0000i >> (5+i*2) * (8+5j) ans = 30.0000 +41.0000i >>
History
Descartes was the first to use the term “imaginary” number in 1637. However, imaginary numbers were invented much earlier by Gerolamo Cardano in the 1500s but they were not widely accepted until the work of Leonhard Euler (1707–1783) and Carl Friedrich Gauss(1777–1855).
In 1843 a mathematical physicist, William Rowan Hamilton, extended the idea of an axis of imaginary numbers in the plane to a three-dimensional space of quaternion imaginaries.
With the development of quotients of polynomial rings, the concept behind an imaginary number became more substantial, but then one also finds other imaginary numbers such as the j of tessarines which has a square of +1. This idea first surfaced with the articles byJames Cockle beginning in 1848.
Powers of i
The powers of i repeat in a cycle:
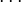

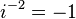

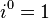


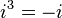

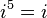

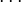
This can be expressed with the following pattern where n is any integer:




This leads to the conclusion that

http://en.wikipedia.org/wiki/Imaginary_number


