Welcome to my Mathematics World - Rhind Matematik Papirüsü

Rhind Mathematical Papyrus

The Rhind Mathematical Papyrus (RMP) (also designated as: papyrus British Museum10057, and pBM 10058), is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 B.C. The British Museum, where the papyrus is now kept, acquired it in 1864 along with the Egyptian Mathematical Leather Roll, also owned by Henry Rhind; there are a few small fragments held by theBrooklyn Museum in New York. It is one of the two well-known Mathematical Papyri along with the Moscow Mathematical Papyrus. The Rhind Papyrus is larger than the Moscow Mathematical Papyrus, while the latter is older than the former. [1]

The Rhind Mathematical Papyrus dates to the Second Intermediate Period of Egypt and is the best example of Egyptian mathematics. It was copied by the scribe Ahmes (i.e., Ahmose; Ahmes is an older transcription favoured by historians of mathematics), from a now-lost text from the reign of king Amenemhat III (12th dynasty). Written in the hieraticscript, this Egyptian manuscript is 33 cm tall and over 5 meters long, and began to be transliterated and mathematically translated in the late 19th century. In 2008, the mathematical translation aspect is incomplete in several respects. The document is dated to Year 33 of the Hyksos king Apophis and also contains a separate later Year 11 on its verso likely from his successor, Khamudi.[2]

In the opening paragraphs of the papyrus, Ahmes presents the papyrus as giving “Accurate reckoning for inquiring into things, and the knowledge of all things, mysteries...all secrets”.

Mathematical problems

The papyrus begins with the RMP 2/n table and follows with 84 problems, written on both sides. Taking up roughly one third of the manuscript is the RMP 2/n table which expresses 2 divided by the odd numbers from 5 to 101 in a sum of Egyptian fractions using Egyptian multiplication and division methods. The sum given in the papyrus optimized to use few fractions, but it does not always use the sum with the fewest fractions.

Several methods by which the scribe may have composed the table have been proposed. An early reporting of the 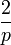$frac{2}{p}$ method was noted by F. Hultsch in 1895, and confirmed by E.M. Bruins in 1945. Today it is called the H-B method. The $frac{2}{pq}$ method consisted of one LCM. Ahmes practiced selecting optimal LCMs. A non-optimal version of the method is found in the Egyptian Mathematical Leather Roll. 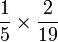The optimal LCM method did not convert $frac{2}{95}$ into $frac{1}{5} times frac{2}{19}$ , with $frac{2}{19}$ as the H-B Method projected in 1895. Ahmes' actual method converted 2/95 by selecting the least common multiple 12, written as 12/12, by writing out:

$frac{2}{95}$ * $frac{12}{12}$ = $frac{24}{1140}$ = $frac{19 + 3 + 2}{1140}$ = $frac{1}{60}$ + $frac{1}{380}$ + $frac{1}{570}$

Ahmes listed the additive (19 + 3 + 2) numerator information in shorthand notes, omitting important steps. Ahmes omissions had confused math historians for over 100 years.

The RMP's 87 problems began with six division-by-10 problems, the central subject of theReisner Papyrus. There are 15 problems dealing with addition, and 18 algebra problems. There are 15 algebra problems of the same type. They ask the reader to find x and a fraction of x such that the sum of x and its fraction equals a given integer. Problem #24 is the easiest, and asks the reader to solve this equation, x + 1/7x = 19. Ahmes, the author of the RMP, worked the problem this way:

(8/7)x = 19, or x = 133/8 = 16 + 5/8,

with 133/8 being the initial vulgar fraction find 16 as the quotient and 5/8 as the remainder term. Ahmes converted 5/8 to an Egyptian fraction series by (4 + 1)/8 = 1/2 + 1/8, making his final quotient plus remainder based answer x = 16 + 1/2 + 1/8.

The algebra problems, from RMP 21 -34, produced increasingly difficult vulgar fractions. RMP 38 converted a hekat, written 320 ro, by multiplying by 35/110, 7/22, obtaining 101 9/11. The initial 320 ro was obtained by multiplying 101 9/11 by 22/7. RMP 82 partitioned a hekat written as (64/64). Hekat unity problems limited n to 1/64 < n < 64, obtaining quotient (Q) and remainder (R) two-part numbers: Q/64 + (5R/n)ro. Ro answers were converted to a one-part 1/10 hekat hin unit by writing 10/n (29 times). Vulgar fractions were easily converted to an optimal (short and small last term) Egyptian fraction series in all RMP problems.

Two arithmetical progressions (A.P.) were solved, one being RMP 64. The method of solution followed the method defined in the Kahun Papyrus. The problem solved sharing 10 hekats of barley, between 10 men, by a difference of 1/8th of a hekat finding 1 7/16 as the largest term.

The second A.P. was RMP 40, the problem divided 100 loaves of bread between five men such that the smallest two shares (12 1/2) were 1/7 of the largest three shares' sum (87 1/2). The problem asked Ahmes to find the shares for each man, which he did without finding the difference (9 1/6) or the largest term (38 1/3). All five shares 38 1/3, 29 1/6, 20, 10 2/3 1/6, and 1 1/3) were calculated by first finding the five terms from a proportional A.P. that summed to 60. The median and the smallest term, x1, were used to find the differential and each term. Ahmes then multiplied each term by 1 2/3 to obtain the sum to 100 A.P. terms. In reproducing the problem in modern algebra, Ahmes also found the sum of the first two terms by solving x + 7x = 60.

The RMP continues with 5 hekat division problems from the Akhmim Wooden Tablet, 15 problems similar to ones from the Moscow Mathematical Papyrus, 23 problems from practical weights and measures, especially the hekat, and three problems from recreational diversion subjects, the last the famous multiple of 7 riddle, written in the Medieval era as, "Going to St. Ives".

The Rhind Mathematical Papyrus also contains the following problem related totrigonometry:[3]

"If a pyramid is 250 cubits high and the side of its base 360 cubits long, what is itsseked?"

The solution to the problem is given as the ratio of half the side of the base of the pyramid to its height, or the run-to-rise ratio of its face. In other words, the quantity he found for the seked is the cotangent of the angle to the base of the pyramid and its face.[3]

Mathematical knowledge

Upon closer inspection, modern-day mathematical analyses of Ahmes' problem-solving strategies reveal a basic awareness of composite and prime numbers;[4] arithmetic,geometric and harmonic means;[4] a simplistic understanding of the Sieve of Eratosthenes [4], and perfect numbers.[4][5]

The papyrus also demonstrates knowledge of solving first order linear equations [5] and summing arithmetic and geometric series.[5]

The papyrus calculates π as $(8/9)^2*4 simeq 3.1605$ (a margin of error of less than 1%). In addition 255/81 was considered (3.1481481...) and 22/7. In RMP 38, Ahmes multiplied a hekat, 320 ro, by 7/22 obtaining 101 9/11. The divisor 7/22 was inverted to 22/7 and multiplied by 101 9/11 obtaining 320 ro as a proof. Ahmes' use of 22/7 may have corrected the hekat's built-in loss based on using 256/81 as pi.

Other problems in the Rhind papyrus demonstrate knowledge of arithmetic progressions(Kahun Papyrus), algebra and geometry.

The papyrus demonstrates knowledge of weights and measures, business distributions of money (paid out in arithmetic progressions, with one group proportionally being paid more than another), and several recreational diversions.